Quick Sort

• Quick sort is a widely used sorting algorithm known for its efficiency and effectiveness.
• It follows the “divide and conquer” approach to sort elements.

Concept

Partitioning

• Choose a pivot element from the array.
• Usually, this can be the first, last, or middle element of the array.
• The goal of partitioning is to rearrange the elements of the array so that all elements less than the pivot are placed before it, and all elements greater than the pivot are placed after it.

Recursion

• Recursively apply the above process to the sub-arrays formed by partitioning until the entire array is sorted.

Combine

• Since each partitioning step places one element (the pivot) into its final sorted position, after all partitions are done, the array is sorted.

Implementation

• Program.cs

namespace QuickSort;

class Program
{
    public static void Main(string[] args)
    {
        int[] arr = { 1, 10, 5, 8, 7, 6, 4, 3, 2, 9 };
        Console.WriteLine("Original array : ");
        Common.Print(arr);
        Console.WriteLine();

        Console.WriteLine("Choose pivot: ");
        Console.WriteLine("[1] First as pivot");
        Console.WriteLine("[2] Middle as pivot");
        Console.WriteLine("[3] Last as pivot");
        var choice = Console.ReadLine();
        Console.WriteLine();

        switch (choice)
        {
            case "1":
                FirstAsPivot.Run(arr);
                break;
            case "2":
                MiddleAsPivot.Run(arr);
                break;
            case "3":
                LastAsPivot.Run(arr);
                break;
            default:
                Console.WriteLine("Choose 1 to 3");
                return;
        }

        Console.WriteLine();
        Console.WriteLine("Sorted array : ");
        Common.Print(arr);
    }
}

• Common.cs

namespace QuickSort
{
    public class Common
    {
        public static void Swap(int[] arr, int a, int b)
        {
            var temp = arr[a]; 
            arr[a] = arr[b]; 
            arr[b] = temp;
        }

        public static void Print(int[] arr)
        {
            foreach(var item in arr)
            {
                Console.Write(item + " ");
            }
            Console.WriteLine();
        }
    }
}

First element as pivot

• FirstAsPivot.cs

namespace QuickSort
{
    public class FirstAsPivot
    {
        public static int[] Run(int[] arr) 
        {
            QuickSort(arr, 0, arr.Length - 1);

            return arr;
        }

        private static void QuickSort(int[] arr, int start, int end)
        {
            if (start >= end) return;

            int pivot = start;
            int left = start + 1;
            int right = end;
            int temp;

            while(left <= right) 
            {
                while (left <= end && arr[left] < arr[pivot] ) left++;
                while (right > start && arr[right] > arr[pivot] ) right--;

                if (left > right) Common.Swap(arr, pivot, right);
                else Common.Swap(arr, left, right);

                Common.Print(arr);
            }

            QuickSort(arr, start, right - 1);
            QuickSort(arr, right + 1, end);
        }
    }
}

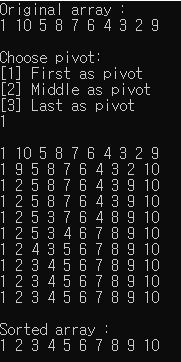
• Round 1
• Index pivot is 0 and pivot value 1. Index left is 1 and left value is 10. Index right is 9 and right value is 9.
• Compare 1 and 10. 10 is bigger then 1. So, index left is 1 and left value is 10 for swapping.
• Compare 1 and 9. Honestly, 1 is smaller then every elements. So, we should move index right until 0 and result right value is 1 for swapping.

• It will swap 1 to 1. So, nothing ganna be changed.

• Round 2

• In first recursive, start is 1 and end is -1. So, it will return directly.

• Round 3
• In second recursive, start is 1 and end is 9.
• Index pivot is 1 and pivot value is 10. Index left is 2 and left value is 5. Index right is 9 and right value is 9.
• Compare 10 and 5. Honestly, 10 is bigger then every elements. So, we should move index left until 10.
• Compare 10 and 9. 9 is smaller then 10. So, index right is 9 and right value is 9 for swapping.
• Compare index left and right. I mean, compare 10 and 9. 10 is bigger then 9. So, swap pivot and right.

• Now our array is 1, 9, 5, 8, 7, 6, 4, 3, 2, 10.

• Round 4
• In third recursive, start is 1 and end is 8.
• After continuing quick sort, you will get 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 as a result of quick sort.

Middle element as pivot

• MiddleAsPivot.cs

namespace QuickSort
{
    public class MiddleAsPivot
    {
        public static int[] Run(int[] arr)
        {
            QuickSort(arr, 0, arr.Length - 1);

            return arr;
        }

        private static void QuickSort(int[] arr, int start, int end)
        {
            if (start >= end) return;

            int left = start;
            int right = end;
            int pivot = (start + end)/2;

            while (left <  right)
            {
                while (arr[left] < arr[pivot]) left++;
                while (arr[right] > arr[pivot]) right--;

                if (left < right)
                {
                    Common.Swap(arr, left, right);
                    Common.Print(arr);
                }
            }

            QuickSort(arr, start, pivot);
            QuickSort(arr, pivot + 1, end);
        }
    }
}

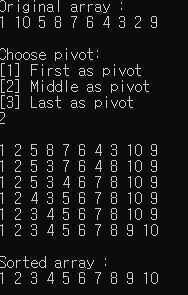
• Round 1
• Index pivot is 4 and pivot value 7. Index left is 0 and left value is 1. Index right is 9 and right value is 9.
• Compare 7 and 1. 1 is smaller then 7. So, move left. Now, index left is 1 and left value is 10.
• Compare 7 and 10. 10 is bigger then 7. So, index left is 1 and left value is 10 for swapping.
• Compare 7 and 9. 9 is bigger then 7. So, move right. Now, index right is 8 and left value is 2.
• Compare 7 and 2. 2 is smaller then 7. So, index right is 8 and right value is 2 for swapping.
• Swap 10 and 2. Our current array is 1, 2, 5, 8, 7, 6, 4, 3, 10, 9.
• Compare 7 and 2. 2 is smaller then 7. So, move left. Now, index left is 2 and left value is 5.
• Compare 7 and 5. 5 is smaller then 7. So, move left. Now, index left is 3 and left value is 8.
• Compare 7 and 8. 8 is bigger then 7. So, index left is 3 and left value is 8 for swapping.
• Compare 7 and 10. 10 is bigger then 7. So, move right. Now, index right is 7 and left value is 3.
• Compare 7 and 3. 3 is smaller then 7. So, index right is 7 and right value is 3 for swapping.
• Swap 8 and 3. Our current array is 1, 2, 5, 3, 7, 6, 4, 8, 10, 9.
• Compare 7 and 3. 3 is smaller then 7. So, move left. Now, index left is 4 and left value is 7.
• Compare 7 and 7. It’s same. So, index left is 4 and left value is 7 for swapping.
• Compare 7 and 8. 8 is bigger then 7. So move right. Now, index right is 6 and right value is 4.
• Compare 7 and 4. 4 is smaller then 7. So, index right is 6 and right value is 4 for swapping.
• Swap 7 and 4. Our current array is 1, 2, 5, 3, 4, 6, 7, 8, 10, 9.

• Move left and right. Current index left is 5 and index right is also 5. Therefore, while loops are finished here.

• Round 2
• In first recursive, start is 0 and end is 4.
• Index pivot is 2 and pivot value 5. Index left is 0 and left value is 1. Index right is 4 and right value is 4.
• Compare 5 and 1. 1 is smaller then 5. So, move left. Now, index left is 1 and left value is 2.
• Compare 5 and 2. 2 is smaller then 5. So, move left. Now, index left is 2 and left value is 5.
• Compare 5 and 5. It’s same. So, index left is 2 and left value is 5 for swapping.
• Compare 5 and 4. 4 is smaller then 5. So, index right is 4 and right value is 4 for swapping.
• Swap 5 and 4. Our current array is 1, 2, 4, 3, 5, 6, 7, 8, 10, 9.
• Compare 4 and 4. It’s same. So, index left is 2 and left value is 4 for swapping.
• Compare 4 and 5. 5 is bigger then 4. So, move right. Now, index right is 3 and right value is 3.

• Swap 4 and 3. Our current array is 1, 2, 3, 4, 5, 6, 7, 8, 10, 9.

• Round 3

• In second recursive, start is 0 and end is 2. But, every elemtns are already sorted.

• Round 4
• In third recursive, start is 0 and end is 1. But, every elemtns are already sorted.
• After continuing quick sort, you will get 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 as a result of quick sort.

Last element as pivot

• LastAsPivot.cs

namespace QuickSort
{
    public class LastAsPivot
    {
        public static int[] Run(int[] arr)
        {
            QuickSort(arr, 0, arr.Length - 1);
            return arr;
        }

        private static void QuickSort(int[] arr, int start, int end)
        {
            if (start > end) return;

            int pivot = end;
            int left = start;
            int right = end - 1;

            while (left < right)
            {
                while (left < end && arr[left] < arr[pivot]) left++;
                while (right > start && arr[right] > arr[pivot]) right--;

                if(left > right) Common.Swap(arr, pivot, left);
                else Common.Swap(arr, left, right);

                Common.Print(arr);
            }

            QuickSort(arr, start, left - 1);
            QuickSort(arr, left + 1, end);
        }
    }
}

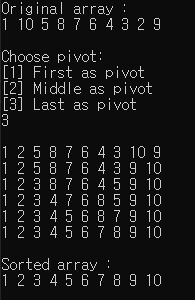
• Round 1
• Index pivot is 9 and pivot value 9. Index left is 0 and left value is 1. Index right is 8 and right value is 2.
• Compare 9 and 1. 1 is smaller then 9. So, move left. Now, index left is 1 and left value is 10.
• Compare 9 and 10. 10 is bigger then 9. So, index left is 1 and left value is 10 for swapping.
• Compare 9 and 2. 2 is smaller then 9. So, index right is 8 and right value is 2 for swapping.
• Swap 10 and 2. Our current array is 1, 2, 5, 8, 7, 6, 4, 3, 10, 9.
• Compare and continue to move. Index left is 8 and left value is 10 for swapping.
• Compare 9 and 10. 10 is bigger then 9. So, move right. Now, index right is 7 and right value is 3.
• Compare 9 and 3. 3 is smaller then 9. So, index right is 7 and right value is 3 for swapping.

• However, index left is bigger then index right. Swap 9 and 10. Our current array is 1, 2, 5, 8, 7, 6, 4, 3, 9, 10.

• Round 2
• In first recursive, start is 0 and end is 7.
• Index pivot is 7 and pivot value 3. Index left is 0 and left value is 1. Index right is 6 and right value is 4.
• Compare 3 and 1. 1 is smaller then 3. So, move left. Now, index left is 1 and left value is 2.
• Compare 3 and 2. 2 is smaller then 3. So, move left. Now, index left is 2 and left value is 5.
• Compare 3 and 5. 5 is bigger then 3. So, index left is 2 and left value is 5 for swapping.
• Compare 3 and continue to move until 2. Index right is 1 and right value is 2 for swapping.

• However, index left is bigger then index right. Swap 5 and 3. Our current array is 1, 2, 3, 8, 7, 6, 4, 5, 9, 10.

• Round 3

• In second recursive, start is 0 and end is 1. But, every elemtns are already sorted.

• Round 4
• In third recursive, start is 0 and end is -1. It will be directly returned.

Download